
Specifically, it is within the red end of the visible spectrum. All observed spectral lines are due to electrons moving between energy levels. (b) The photon emitted will be in the visible light spectrum because it is the first transition of the Balmer Series. What is the Rydberg formula for the spectrum of hydrogen atom The emission spectrum of atomic hydrogen is divided into a number of spectral series, with wavelengths given by the Rydberg formula: 1vacRZ2(1n121n22) 1 v a c R Z 2 ( 1 n 1 2 1 n 2 2 ). (b) What type of radiation is emitted by the drop from n i = 3 to n f = 2? (1 mark) (a) Calculate the frequency of radiation emitted when an electron drops from n i= 3 to n f = 2.
#Rydberg equation calculator series#
Hydrogen shows a large number of spectral lines, the visible ones being part of the Balmer series where n f = 2. Hence, it is often only used for the hydrogen atom.
However, the accuracy of prediction made by Rydberg’s equation rapidly decreases as the atom becomes larger. The number of significant figures in the answer to the following calculation is. Where Z is the number of protons in the atom/ion’s nucleus. 097 x 10-7 m-1 (Rydberg Constant) Multiple Choice (5 points each). Rydberg’s equation quantitatively determines the wavelength of photons in the Balmer series and could be used for other series and atoms. Where λ is the wavelength of emitted radiation, R is Rydberg’s constant (1.097x10 7 m -1), n f and n i are the final and initial energy level during an electron’s transition respectively. In other words, the energy emitted by an electron during spectroscopy equals to the amount absorbed. Therefore, when an electron returns to a lower energy level, it must emit the exact amount of energy it first absorbed to reach that energy level. Conservation of energy – Bohr postulated that an electron is a discrete orbit (energy level) does not emit energy. In this equation the Rydberg constant was introduced (R = 1.097x10 7 m -1) and is known as the Rydberg Equation: Johannes Rydberg formula describes the wavelengths of light emitted during an electronic transition between different energy levels/ shells of the atom. Using Bohr's postulates and some manipulation of mathematics, Rydberg later was able to create the same formula which Balmer has derived. Balmer's initial equation was first devised through empirically examining the lines in the hydrogen spectrum and creating a formula for them to fit in. 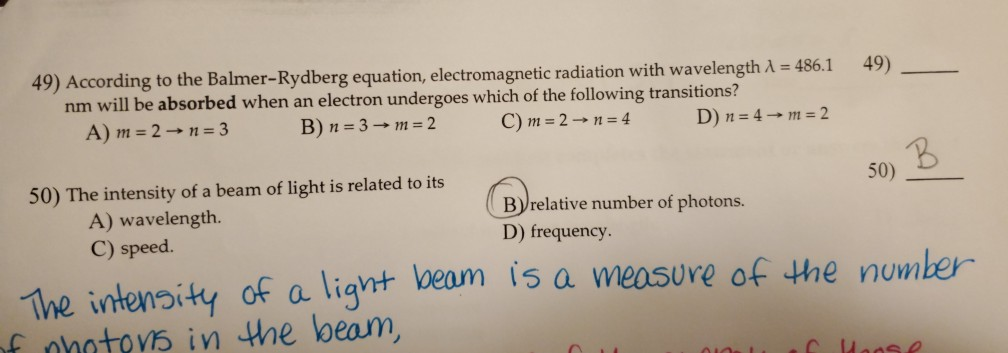

relate qualitatively and quantitatively the quantised energy levels of the hydrogen atom and the law of conservation of energy to the line emission spectrum of hydrogen using:.





 0 kommentar(er)
0 kommentar(er)
